简介
SymPy 是一个开源的符号计算Python库,SymPy采用了宽松的BSD开源协议,并且完全免费。它的目标是成为一个全功能的计算机代数系统(CAS),同时保持代码尽可能简单,以便于理解和扩展。
本学习笔记参考官方的教程:https://docs.sympy.org/latest/tutorials
安装与基本使用
如果你使用Anacoda,无需安装,Anacoda内置了SymPy。
TIP推荐使用micromamba代替Anacoda,它更轻量,也更快速。且默认使用conda-forge源。
Terminal window
如果你使用pip:
pip install sympy前置芝士
会Python就行。数学水平因人而异,根据自己的需要选用相应的功能。
什么是符号计算?
前面提到,SymPy是一个 符号计算 库,那么什么是符号计算。符号计算(Symbolic Computation),就是在计算机上用符号精确表示数学对象,而不是得到一个近似的数值解。
看一个例子:
>>>import math>>>math.sqrt(8)2.8284271247461903Python的math库给出的计算的结果是,然而实际上,这只是的一个近似值,我们知道,它的精确值是不能用有限的小数表示的。
而在SymPy中:
>>> from sympy import *>>> sqrt(8)2*sqrt(2)SymPy给我们的结果是,这才是一个精确的化简的结果。在SymPy中,非完全平方数的平方根默认会被保留。
定义符号与计算
在SymPy中,符号需要在使用前用Symbol()或symbols()来定义:
a = Symbol('a')x, y = symbols('x y')# symbols接受一系列用空格或逗号隔开的符号,返回对应的变量最好将变量名设置得与符号名一致,方便记忆和使用。除非符号中包含了Python不允许的符号,或者符号名太长,想使用一个短一点的变量名来表示。
SymPy支持直接使用+、-、*、/、**来操作这些符号。
>>> x, y = symbols("x y")>>> expr = x + 2*y>>> exprx + 2*y>>> expr + 1 - x2*y + 1>>> expr / 2x/2 + y输入x * expr你会发现SymPy并没有为我们展开表达式为x**2 + 2*x*y,而是保留了x*(x + 2*y)的形式。因为因式分解是SymPy默认的化简操作,你也可以利用expand来展开,用factor来分解。
>>> expand(x * expr)x**2 + 2*x*y>>> factor(2*x**2 - 7*x - 4)(x - 4)*(2*x + 1)SymPy计算出了展开的结果,和因式分解的结果。
输出
可以通过调整一些选项改变SymPy输出的格式。
用init_printing(use_unicode=True)可以允许SymPy使用Unicode输出。
计算
>>> init_printing(use_unicode=False)>>> integrate(sin(x**2), (x, -oo, oo)) ___ ____\/ 2 *\/ pi------------ 2>>> init_printing(use_unicode=True)>>> integrate(sin(x**2), (x, -oo, oo))√2⋅√π───── 2第一个输出中SymPy使用了字符画的方式画出 ,使用了pi表示。第二个输出使用了Unicode字符“√”和“π”。
SymPy还可以使用 :
>>> latex(Integral(cos(x)**2, (x, 0, pi)))\int\limits_{0}^{\pi} \cos^{2}{\left(x \right)}\, dx将\int\limits_{0}^{\pi} \cos^{2}{\left(x \right)}\, dx使用任意一个 编译器编译,就可以得到下面这样漂亮的结果:
符号的替换
用subs(),但注意subs()并不改变原表达式。
>>> expr = cos(x) + 1>>> expr.subs(x, y)cos(y) + 1>>> exprcos(x) + 1也可以替换数字,进行在某一点求值的操作。
>>> expr = sin(2*x) + cos(2*x)>>> expr.subs(x, pi/5)-1/4 + sqrt(5)/4 + sqrt(sqrt(5)/8 + 5/8)也可以替换多个符号
>>> expr = x**3 + 4*x*y - z>>> expr.subs([(x, 2), (y, 4), (z, 0)])40字符串转表达式
用sympify()(不是symplify()
>>> str_expr = "x**2 + 3*x - 1/2">>> expr = sympify(str_expr)>>> exprx**2 + 3*x - 1/2>>> expr.subs(x, 2)19/2表达式转浮点数
用evalf()
>>> expr = sqrt(8)>>> expr.evalf()2.82842712474619默认情况下,会给出15位的精度,但是也可以指定所需要的精度
expr.evalf(100)2828427124746190097603377448419396157139343750753896146353359475981464956924214077700775068655283145如果想要用subs()进行单点求值后再用evalf()进行数值估计,用expr.evalf(subs={<Symbol>: <Value>})是比expr.subs(<Symbol>, <Value>).evalf()更推荐的方法。因为这样会使计算更高效且稳定。
>>> expr = cos(2*x)>>> expr.evalf(subs={x: 2.4})0.0874989834394464假如指定了chop=True,SymPy会自动移除小于期望精度的舍入误差
>>> one = cos(1)**2 + sin(1)**2>>> (one - 1).evalf()-0.e-124>>> (one - 1).evalf(chop=True)0多点求值
使用SymPy对表达式做多点的求值(比如成千上万点后)是比较慢的。如果有这种需求,可以对表达式lambdify()后交给其他库处理(比如NumPy或SciPy)
>>> import numpy>>> a = numpy.arange(10)>>> expr = sin(x)>>> f = lambdify(x, expr, "numpy")>>> f(a)array([ 0. , 0.84147098, 0.90929743, 0.14112001, -0.7568025 , -0.95892427, -0.2794155 , 0.6569866 , 0.98935825, 0.41211849])lambdify()将一个SymPy表达式转换成一个计算表达式在某点的值的函数,以便于使用其他库进行计算。
需要避免的坑
坑一:符号与变量
符号(Symbol)指的是SymPy提供的,用symbols()定义的符号,而变量是Python提供的。
>>> x = symbols('x')>>> expr = x + 1>>> x = 2>>> print(expr)x + 1以上这个程序,并没有输出3,而是输出了x + 1,这是因为x = 2只是将变量x的值,从符号,变成了数字2,而符号并没有发生改变,因此expr的值也就没有改变。
想要计算expr在x=2条件下的值,可以使用subs:
>>> x = symbols('x')>>> expr = x + 1>>> expr.subs(x, 2)3坑二:等于号
假如你用==检测两个式子是否相等,你将会得到错误的结果:
>>> (x + 1)**2 == x**2 + 2*x + 1FalseSymPy并没有扩展Python的语法,=依然表示赋值,==表示变量的相等,因此在SymPy中,主要用这两种方式表示两个式子相等:
-
这是官方文档中推荐的方法:假如你想要验证是否成立,可以检测是否成立,只要将两个式子相减,然后使用
simplify()函数化简,如果结果是0,则必定相等,如果不是0,大多数情况下不相等,但也存在极少数情况,式子确实为0,但是SymPy无法将其化简,对于常见的数学式子,可以放心地使用这个方法检验其是否相等。>>> a = (x + 1)**2>>> b = x**2 + 2*x + 1>>> simplify(a - b)0>>> c = x**2 - 2*x + 1>>> simplify(a - c)4*x -
另一种方法是使用
a.equals(b),但是这个方法并不是使用式子的化简得到的结论,而是通过随机地给式子赋多个值,比较二者是否相等。>>> a = cos(x)**2 - sin(x)**2>>> b = cos(2*x)>>> a.equals(b)True
坑三:^符号
SymPy使用和Python一样的符号约定,用**表示指数,^表示异或(Xor),所以不应该尝试使用^表示指数。
>>> Xor(x, y)x ^ y坑四:/符号
两个SymPy对象相除,或者一个SymPy对象相除的时候,返回值都是SymPy对象,这没有问题。但是当分子分母都是Python的int时,要小心了。两个SymPy对象相除会返回一个分数,但是两个Python的int相除会返回一个浮点数(Python3)。
>>> x / yx/y>>> x / 19x/19>>> 3 / x3/x>>> 3 / 190.157894736842105250.15789473684210525不是我们想要的结果,这个值不是精确的,当处理两个整数相除的时候,可以使用Rational()来避免这种结果:
Rational(3, 19)3/19如果和其他符号连接起来的时候这种错误就更难以察觉:
>>> x + 1/3x + 0.333333333333333>>> x + Rational(1, 3)x + 1/3输出
初始化
init_printing()会为你启用当前环境下可用的最佳的输出效果。
from sympy import init_printinginit_printing()如果你使用交互式命令行,init_session() 函数将自动导入SymPy中的所有内容,创建一些常用符号,设置绘图,并运行 init_printing()。
>>> from sympy import init_session>>> init_session()Python console for SymPy 0.7.3 (Python 2.7.5-64-bit) (ground types: gmpy)
These commands were executed:>>> from __future__ import division>>> from sympy import *>>> x, y, z, t = symbols('x y z t')>>> k, m, n = symbols('k m n', integer=True)>>> f, g, h = symbols('f g h', cls=Function)>>> init_printing() # doctest: +SKIP
Documentation can be found at https://www.sympy.org/用Jupyter美化输出
但是终端的输出效果实在是有点丑
这是设置了init_printing(use_unicode=False),不允许使用Unicode字符的输出
>>> Integral(sqrt(1/x), x) / | | ___ | / 1 | / - dx | \/ x |/这是设置了init_printing(use_unicode=True),允许使用Unicode字符的输出
>>> Integral(sqrt(1/x), x)⌠⎮ ___⎮ ╱ 1⎮ ╱ ─ dx⎮ ╲╱ x⌡这是Jupyter notebook里的输出,使用了MathML渲染的:
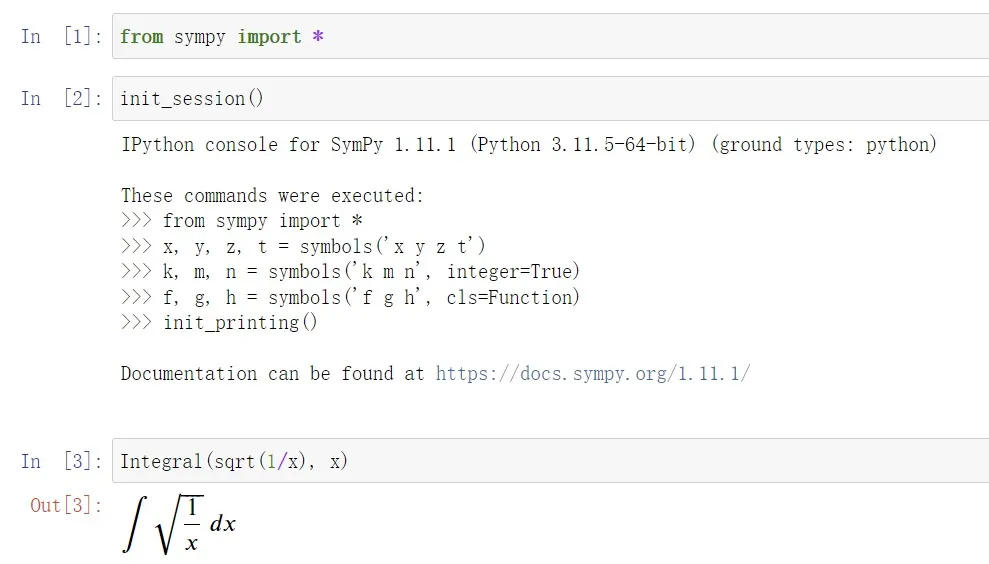
NOTE确保你安装好了Jupyter Notebook,在Jupyter中才能达成上面的效果
输出了很漂亮的公式,以后都可以这样使用。
化简
SymPy中的 simplify() 可以进行智能的化简

但是,simplify() 的输出有时候会和你的预想不同,因为并没有“最简”并没有一个严格的定义。

想要得到 应该使用 factor()。
而且,simplify() 会调用多种化简函数,为了方便,一般在交互式界面里使用 simplify() 。如果在程序里使用,会造成运行效率低下。当你知道需要化简成什么形式时,应该使用对应的化简函数。这样不仅运行快,而且输出的格式是固定的。
一些常用的化简函数
-
expand()展开,如 -
factor()因式分解,如如果希望得到所有因子的列表,用
factor_list() -
collect(expr, x)将x作为主元整理expr。如 -
cancel()对分子分母自动消去共同因子,如 -
apart()会执行部分因式分解(Partial fraction decomposition) -
trigsimp()是三角函数版本的simplify()会智能地化简三角函数表达式。 -
expand_trig()会使用和差角、二倍角等公式展开表达式,如 -
expr.rewrite(function)尝试用function表示expr,如
SymPy中的化简函数还有很多,这里只是一些常用的。
微积分
SymPy提供了完善的微积分支持:
求导
diff(expr, x)可以求expr关于x的导数,也可以写成expr.diff(x)。
diff(expr, x,x, x)可以对x求三阶导,也可以写成diff(expr, x,3)或expr.diff(x, 3)。
Derivative()可以创建一个导数但不计算它

对未计算的导数使用.doit()可以计算它。
积分
integrate(exp(-x), (x, 0, oo))将会计算
其中oo是两个“o”,用来表示无穷大。
integrate(exp(-x**2 - y**2), (x, -oo, oo), (y, -oo, oo))将会计算
和上面求导一样,Integral会创建一个积分但是不计算它,.doit()可以计算未计算的积分。
极限
limit(sin(x)/x, x, 0)将会计算
计算单侧极限,可以向第三个参数传入'+'或'-'。limit(1/x, x, 0, '-')将会计算
同上,Integral会创建一个未计算的极限,.doit()可以计算它。
计算某点处的级数展开
用expr.series(x, a, n)会给出表达式在 x = a 处的 n 阶展开。

不想要那个表示余项的O,就用.removeO()

解方程
求解方程
在前面已经提到过,SymPy中表达相等应该用Eq()而不是==或=
用solveset(equation, x)可以求equation关于x的解集,如果等式右边是0,也可以不写成solveset(Eq(expr, 0), x),直接写成solveset(expr, x),例如:
>>> solveset(Eq(x**2, 1), x){-1, 1}>>> solveset(x**2 - 1, x){-1, 1}如果无解,将返回 ,如果无法求解,会返回一个条件集合。
>>> solveset(exp(x), x) # 无解∅>>> solveset(cos(x) - x, x) # 无法求解{x │ x ∊ ℂ ∧ (-x + cos(x) = 0)}求解线性方程组
使用linsolve()
>>> linsolve([x + y + z - 1, x + y + 2*z - 3 ], (x, y, z)) # 等式列表形式{(-y - 1, y, 2)}>>> linsolve(Matrix(([1, 1, 1, 1], [1, 1, 2, 3])), (x, y, z)) # 增广矩阵形式{(-y - 1, y, 2)}>>> M = Matrix(((1, 1, 1, 1), (1, 1, 2, 3))) # A*x = b 形式system = A, b = M[:, :-1], M[:, -1]linsolve(system, x, y, z){(-y - 1, y, 2)}求解非线性方程组
使用nonlinsolve()

获得多项式的重根数
solveset()返回的都是不重复的根,要获得多项式的重根数,可以使用roots()
>>> solveset(x**3 - 6*x**2 + 9*x, x){0, 3}>>> roots(x**3 - 6*x**2 + 9*x, x){0: 1, 3: 2}求解微分方程
使用dsolve()
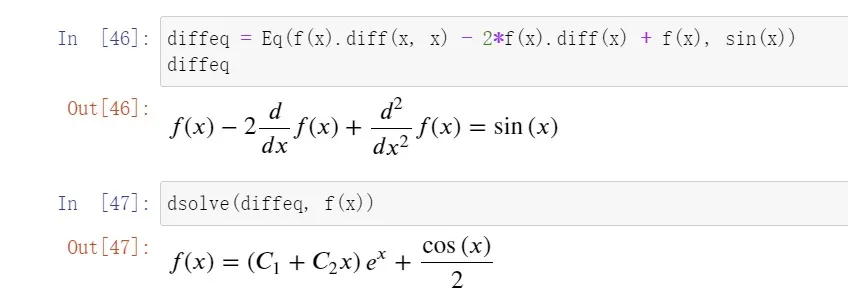
矩阵
Matrix()可以创建矩阵,参数是一个二维数组。如果传入了一维数组,默认会生成一个列向量。

与 SymPy 中的其他对象不同,Matrix 是可变的。这意味着它们可以就地修改。这样的缺点是 Matrix 不能用于需要不可变的地方,例如其他 SymPy 表达式内部或作为字典的键。要用不可变版本的 Matrix,可以使用 ImmutableMatrix。
shape(M)返回一个元组,描述了矩阵的形状。
.row(0)可以得到第一行,.col(-1)可以得到最后一列,负数下标倒序访问这一点和 Python 中的数组是一样的。
.col_del()和“.row_del()可以删除行或列。.row_insert和.col_insert`可以插入行或列。
>>> M.col_del(0)>>> M⎡2 3⎤⎢ ⎥⎣0 4⎦>>> M.row_del(1)>>> M[2 3]>>> M[2 3]>>> M = M.row_insert(1, Matrix([[0, 4]]))>>> M⎡2 3⎤⎢ ⎥⎣0 4⎦>>> M = M.col_insert(0, Matrix([1, -2]))>>> M⎡1 2 3⎤⎢ ⎥⎣-2 0 4⎦基本操作
+ * **,分别代表加法,乘法和乘方,矩阵求逆就是M**-1
M.T返回矩阵的转置。
eye(n)、ones(n, m)、zeros(n, m)分别可以用来创建单位矩阵、全1矩阵和零矩阵。
diag()可以创建对角矩阵
>>> diag(-1, ones(2, 2), Matrix([5, 7, 5]))⎡-1 0 0 0⎤⎢ ⎥⎢0 1 1 0⎥⎢ ⎥⎢0 1 1 0⎥⎢ ⎥⎢0 0 0 5⎥⎢ ⎥⎢0 0 0 7⎥⎢ ⎥⎣0 0 0 5⎦其他操作
-
行列式:
.det() -
转化为简化行阶梯矩阵:
.rref(),返回一个元组,第一个元素是简化行阶梯矩阵,第二个元素是一个存放了阶梯头所在列的列标的元组。
-
子空间:
.nullspace()零空间、.columnspace()列空间、rowspace()行空间。 -
.eigenvals()特征值、.eigenvects()特征向量、.charpoly(lamda)特征多项式、.diagonalize()对角化。
一个实例
矩阵是一个线性方程组的增广矩阵,问取多少的时候,该方程组有解?
输入以下代码,即可解出,当 或 时方程组有解。
a, x1, x2, x3 = symbols('a x1 x2 x3')A = Matrix([ [1, 2, 3], [2, -1, -2], [-1, -7, -11]])b = Matrix([4, a**2, a])x = Matrix([x1, x2, x3])solve(A*x - b)
